明道云的javascript能不能实现EXCLE的IRR函数效果？

云柚子 2024-02-01 10:20:20 问答收藏

8 / 447

云柚子 2024-02-01 10:20:20 回复

Alvin.Zhang 2024-01-07 15:00:43

现在百川智能还行，不要钱，你可以试试让它帮你写，当然效果可能没有 ChatGPT 好，得多调试几次

我自己写了 JavaScript 实现了

Alvin.Zhang 2024-01-07 15:00:43 回复

现在百川智能还行，不要钱，你可以试试让它帮你写，当然效果可能没有 ChatGPT 好，得多调试几次

云柚子 2024-01-05 17:59:10 回复

张春泉（Team） 2024-01-03 20:58:41

这种问题，明道云 AI 生成代码块，给你答案，加分项 😄

def calculate_irr(cashflows):  
    n = len(cashflows)  
    if n == 0:  
        return 0.0  
  
    # 初始化IRR的猜测值  
    irr_guess = 0.1  # 可以根据需要进行调整  
    precision = 0.00001  # 精度要求  
    max_iterations = 1000  # 最大迭代次数以防止无限循环  
  
    # 使用牛顿-拉弗森方法迭代计算IRR  
    for _ in range(max_iterations):  
        npv = 0  
        for i in range(n):  
            npv += cashflows[i] / pow(1 + irr_guess, i + 1)  
  
        # 如果NPV足够接近0，则返回当前的IRR猜测值  
        if abs(npv) < precision:  
            return irr_guess  
  
        # 计算下一轮的IRR猜测值  
        derivative = 0  
        for i in range(n):  
            derivative -= (i + 1) * cashflows[i] / pow(1 + irr_guess, i + 2)  
  
        irr_guess -= npv / derivative  
  
    # 如果达到最大迭代次数而没有找到解决方案，则返回None或抛出异常  
    raise ValueError("无法在给定的迭代次数内计算IRR")
cl= [-10000, 2500, 2500, 2500, 2500, 2500]  
output={'a':calculate_irr(cl)}

为啥我用 AI 生成的代码块，计算 EXCLE 的 MIRR 函数，和 EXCLE 里面的 MIRR 函数结果不同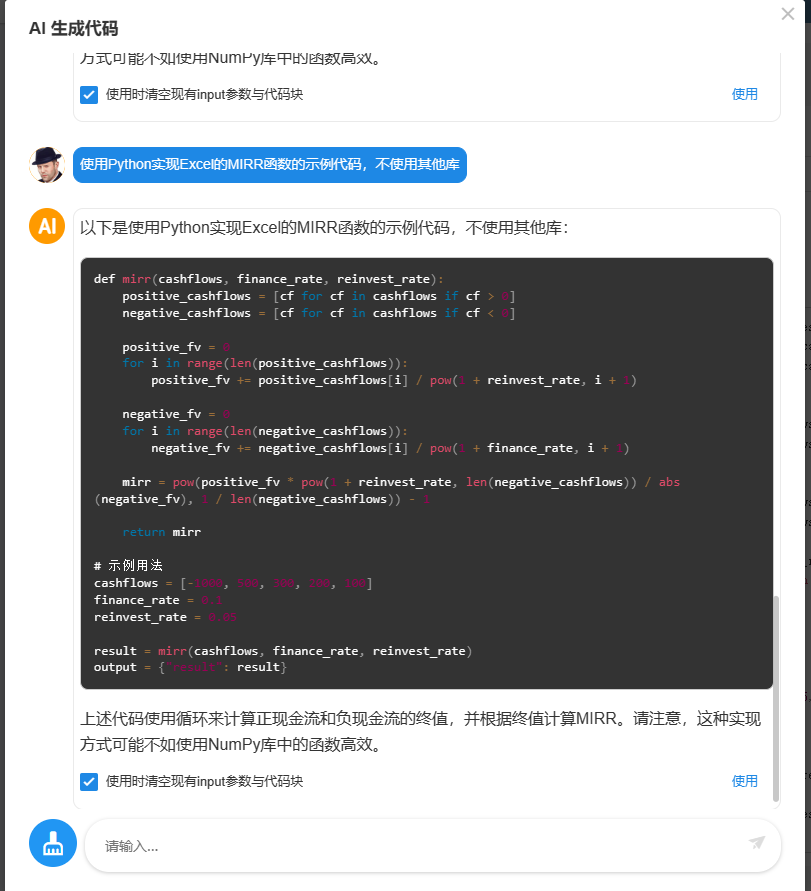微信图片_20240105175815.png
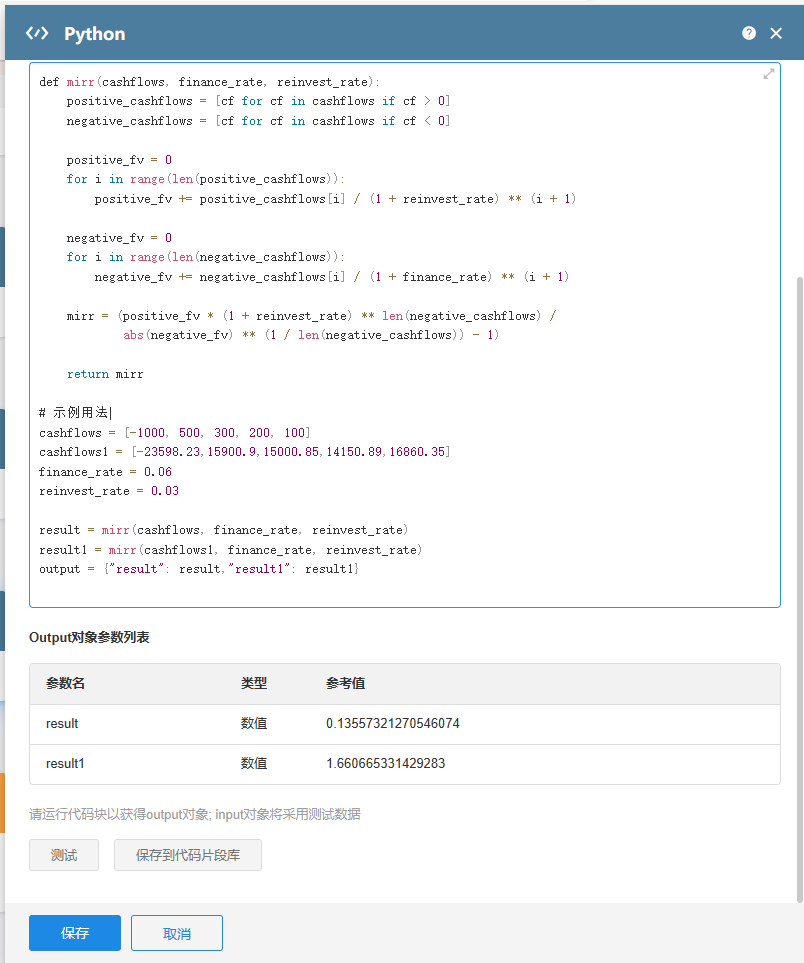
微信图片_20240105175838.png
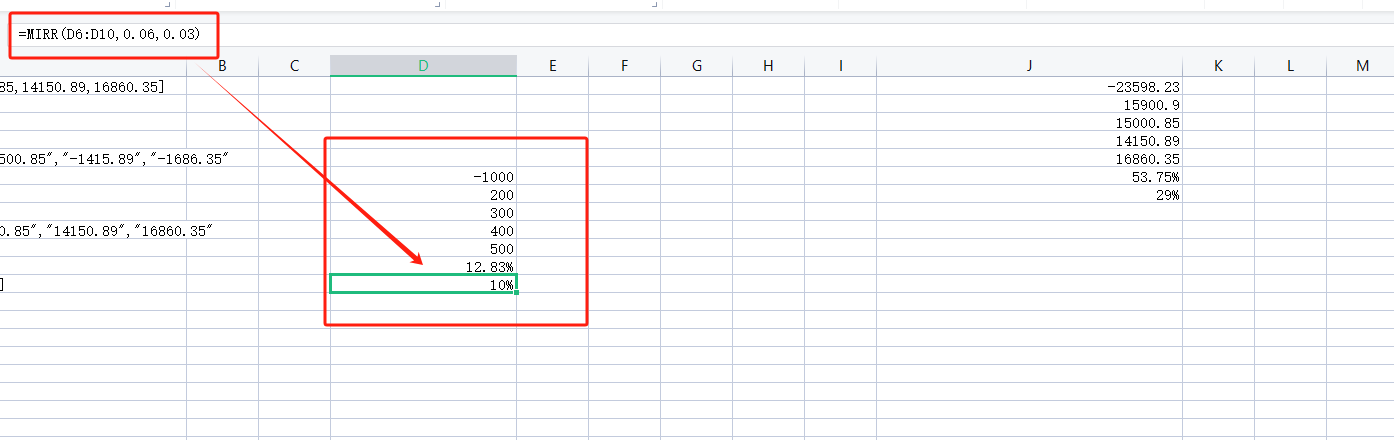
微信图片_20240105175841.png

Q 2024-01-04 08:37:48 回复

张春泉（Team） 2024-01-03 20:58:41

这种问题，明道云 AI 生成代码块，给你答案，加分项 😄

def calculate_irr(cashflows):  
    n = len(cashflows)  
    if n == 0:  
        return 0.0  
  
    # 初始化IRR的猜测值  
    irr_guess = 0.1  # 可以根据需要进行调整  
    precision = 0.00001  # 精度要求  
    max_iterations = 1000  # 最大迭代次数以防止无限循环  
  
    # 使用牛顿-拉弗森方法迭代计算IRR  
    for _ in range(max_iterations):  
        npv = 0  
        for i in range(n):  
            npv += cashflows[i] / pow(1 + irr_guess, i + 1)  
  
        # 如果NPV足够接近0，则返回当前的IRR猜测值  
        if abs(npv) < precision:  
            return irr_guess  
  
        # 计算下一轮的IRR猜测值  
        derivative = 0  
        for i in range(n):  
            derivative -= (i + 1) * cashflows[i] / pow(1 + irr_guess, i + 2)  
  
        irr_guess -= npv / derivative  
  
    # 如果达到最大迭代次数而没有找到解决方案，则返回None或抛出异常  
    raise ValueError("无法在给定的迭代次数内计算IRR")
cl= [-10000, 2500, 2500, 2500, 2500, 2500]  
output={'a':calculate_irr(cl)}

私有部署用不了，公有云没权限，太可惜了

张春泉（Team） 2024-01-03 20:58:41 回复

这种问题，明道云 AI 生成代码块，给你答案，加分项 😄

def calculate_irr(cashflows):  
    n = len(cashflows)  
    if n == 0:  
        return 0.0  
  
    # 初始化IRR的猜测值  
    irr_guess = 0.1  # 可以根据需要进行调整  
    precision = 0.00001  # 精度要求  
    max_iterations = 1000  # 最大迭代次数以防止无限循环  
  
    # 使用牛顿-拉弗森方法迭代计算IRR  
    for _ in range(max_iterations):  
        npv = 0  
        for i in range(n):  
            npv += cashflows[i] / pow(1 + irr_guess, i + 1)  
  
        # 如果NPV足够接近0，则返回当前的IRR猜测值  
        if abs(npv) < precision:  
            return irr_guess  
  
        # 计算下一轮的IRR猜测值  
        derivative = 0  
        for i in range(n):  
            derivative -= (i + 1) * cashflows[i] / pow(1 + irr_guess, i + 2)  
  
        irr_guess -= npv / derivative  
  
    # 如果达到最大迭代次数而没有找到解决方案，则返回None或抛出异常  
    raise ValueError("无法在给定的迭代次数内计算IRR")
cl= [-10000, 2500, 2500, 2500, 2500, 2500]  
output={'a':calculate_irr(cl)}

云柚子 2024-01-03 16:03:01 回复

Alvin.Zhang 2024-01-03 13:24:49
可以是可以，有点麻烦，不知道对不对，你看看：

在 JavaScript 中实现类似 Excel 中的 IRR（内部收益率）函数可以通过数值分析的方法，例如牛顿-拉夫森方法（Newton-Raphson Method）。这种方法用于求解非线性方程的根。IRR 函数的目的是找到使净现值（NPV）为零的贴现率。

首先，我们需要实现两个函数：一个用于计算净现值（NPV），另一个用于使用牛顿-拉夫森方法找到 IRR。

npv(rate, values) 函数用于计算给定贴现率下的净现值。

irr(values) 函数用于找到使净现值为零的贴现率。

下面是这两个函数的实现代码，每行代码都附有中文注释：
// 计算净现值
function npv(rate, values) {
    // 初始化净现值为0
    let totalValue = 0;
    // 遍历所有现金流
    for (let i = 0; i < values.length; i++) {
        // 根据贴现率和时间计算现值，并累加到总值
        totalValue += values[i] / Math.pow(1 + rate, i);
    }
    // 返回计算出的净现值
    return totalValue;
}

// 使用牛顿-拉夫森方法计算IRR
function irr(values) {
    // 初始估计的IRR值
    let guessRate = 0.1;
    // 允许的误差范围
    const tolerance = 0.00001;
    // 最大迭代次数
    const maxIteration = 1000;
    // 当前迭代次数
    let iteration = 0;
    // 保存上一次迭代的结果
    let lastValue = npv(guessRate, values);

    // 开始迭代
    while (iteration < maxIteration) {
        // 根据当前估计的IRR值计算净现值
        let currentValue = npv(guessRate, values);
        // 计算净现值的变化量（导数）
        let npvDelta = 0;
        for (let i = 1; i < values.length; i++) {
            npvDelta += -i * values[i] / Math.pow(1 + guessRate, i + 1);
        }
        // 检查是否已接近零点
        if (Math.abs(currentValue) < tolerance) {
            return guessRate;
        }
        // 更新IRR估计值
        let newRate = guessRate - currentValue / npvDelta;
        // 如果结果变化不大，则返回当前估计值
        if (Math.abs(newRate - guessRate) < tolerance) {
            return newRate;
        }
        // 准备下一次迭代
        guessRate = newRate;
        lastValue = currentValue;
        iteration++;
    }
    // 如果达到最大迭代次数仍未找到结果，则返回null
    return null;
}
这段代码包括了两个函数。npv 函数接受贴现率和一系列现金流，计算其净现值。irr 函数则试图找到使净现值为零的贴现率，它初始化一个猜测值（这里是 10%），然后通过牛顿-拉夫森方法逐步迭代，直到找到满足条件的贴现率或达到最大迭代次数。

请注意，这种方法可能不会总是收敛到正确的解，特别是当现金流模式非常不规则时。在实际应用中，可能需要对初始猜测值或其他参数进行调整以确保正确性。

好，我试一下看看

Alvin.Zhang 2024-01-03 13:26:20 回复

如果在代码节点里使用，建议用 Python 配合相关科学计算的扩展库

Alvin.Zhang 2024-01-03 13:24:49 回复

可以是可以，有点麻烦，不知道对不对，你看看：

在 JavaScript 中实现类似 Excel 中的 IRR（内部收益率）函数可以通过数值分析的方法，例如牛顿-拉夫森方法（Newton-Raphson Method）。这种方法用于求解非线性方程的根。IRR 函数的目的是找到使净现值（NPV）为零的贴现率。

首先，我们需要实现两个函数：一个用于计算净现值（NPV），另一个用于使用牛顿-拉夫森方法找到 IRR。

npv(rate, values) 函数用于计算给定贴现率下的净现值。
irr(values) 函数用于找到使净现值为零的贴现率。

下面是这两个函数的实现代码，每行代码都附有中文注释：

// 计算净现值
function npv(rate, values) {
    // 初始化净现值为0
    let totalValue = 0;
    // 遍历所有现金流
    for (let i = 0; i < values.length; i++) {
        // 根据贴现率和时间计算现值，并累加到总值
        totalValue += values[i] / Math.pow(1 + rate, i);
    }
    // 返回计算出的净现值
    return totalValue;
}

// 使用牛顿-拉夫森方法计算IRR
function irr(values) {
    // 初始估计的IRR值
    let guessRate = 0.1;
    // 允许的误差范围
    const tolerance = 0.00001;
    // 最大迭代次数
    const maxIteration = 1000;
    // 当前迭代次数
    let iteration = 0;
    // 保存上一次迭代的结果
    let lastValue = npv(guessRate, values);

    // 开始迭代
    while (iteration < maxIteration) {
        // 根据当前估计的IRR值计算净现值
        let currentValue = npv(guessRate, values);
        // 计算净现值的变化量（导数）
        let npvDelta = 0;
        for (let i = 1; i < values.length; i++) {
            npvDelta += -i * values[i] / Math.pow(1 + guessRate, i + 1);
        }
        // 检查是否已接近零点
        if (Math.abs(currentValue) < tolerance) {
            return guessRate;
        }
        // 更新IRR估计值
        let newRate = guessRate - currentValue / npvDelta;
        // 如果结果变化不大，则返回当前估计值
        if (Math.abs(newRate - guessRate) < tolerance) {
            return newRate;
        }
        // 准备下一次迭代
        guessRate = newRate;
        lastValue = currentValue;
        iteration++;
    }
    // 如果达到最大迭代次数仍未找到结果，则返回null
    return null;
}

这段代码包括了两个函数。npv 函数接受贴现率和一系列现金流，计算其净现值。irr 函数则试图找到使净现值为零的贴现率，它初始化一个猜测值（这里是 10%），然后通过牛顿-拉夫森方法逐步迭代，直到找到满足条件的贴现率或达到最大迭代次数。

请注意，这种方法可能不会总是收敛到正确的解，特别是当现金流模式非常不规则时。在实际应用中，可能需要对初始猜测值或其他参数进行调整以确保正确性。

发表话题

云柚子

这家伙很懒，什么都没留下

积分
249
注册排名
2440